Hayden's Archive
[AI/딥러닝] Image Processing / Softmax Function / Loss Function 본문
[AI/딥러닝] Image Processing / Softmax Function / Loss Function
_hayden 2020. 7. 28. 11:09
CIFAR-10는 5만개의 Training Image가 있고 만개의 Test Image가 있음. 각각의 이미지는 32×32×3
| * 32×32×3의 의미 32X32 => 이미지 세로와 가로(보통 정사각형으로 주어짐) 3 => 채널 수. (흑백은 채널이 1개, 칼라는 채널이 3개, RGB) |
입력값인 X로 이미지가 들어옴.
| MNIST - 28X28X1 (0~9 손글씨 숫자. 검정색 바탕에 흰색글씨) 10개의 카테고리 랜덤함수 돌리면 10%의 확률 정답이 나오겠지만 딥러닝 알고리즘 돌리면 정확도 99.8%(사람보다 더 잘 맞힘) |
| MNIST-Fashion |
| CIFAR10 - 32X32X3 -- 정확도 99.3% 10개의 카테고리 MNIST보다 정보량이 더 많다.(=복잡한 입력이다) |
| CIFAR100 - 정확도 93% 100개의 카테고리 카테고리 수가 많을수록 정확도가 떨어짐 |
| 이미지넷 - 정확도 88% 1000개의 카테고리 카테고리 수가 많을수록 정확도가 급격히 떨어짐 |
따라서 카테고리(=라벨, 클래스)는 보통 50개를 넘지 않도록 한다.
실제로 클래스 카테고리가 10개라 하더라도 정확도 99% 안 나옴.
트레이닝 하고자 하는 데이터들은 Toy DataSet -> 낮은 해상도, 낮은 사이즈로 함. 실제 데이터는 해상도도 높고, 사이즈도 큼. 그래서 정보량이 더 많고 실제 데이터 가지고 하면 정확도 99% 안 나오고 정확도 떨어지게 됨.
보통 학술적으로 연구할 때 92%~95%(학사 수준) 이 정도 나오면 잘 나온 것.
하지만 99%대(박사수준)로 올리는 것은 10배 더 어렵다. 비용적인 측면에서도 100배 더 든다.
정확도 올리는 데 가성비를 따져야 함.
50%에서 1% 올리는 건 쉬움.
90%에서 1% 올리는 건 정말 어려움.

32x32x3의 고양이 사진을 입력하려고 할 때 원본이미지가 3차원짜리인데 컴퓨터가 통으로 못 받음. Flattening 해야 함.(평평하게 펴야 함. 1차원으로.)
| x는 입력값(이미지), Y는 출력값(라벨) Y = f(x, W) = Wx+b |
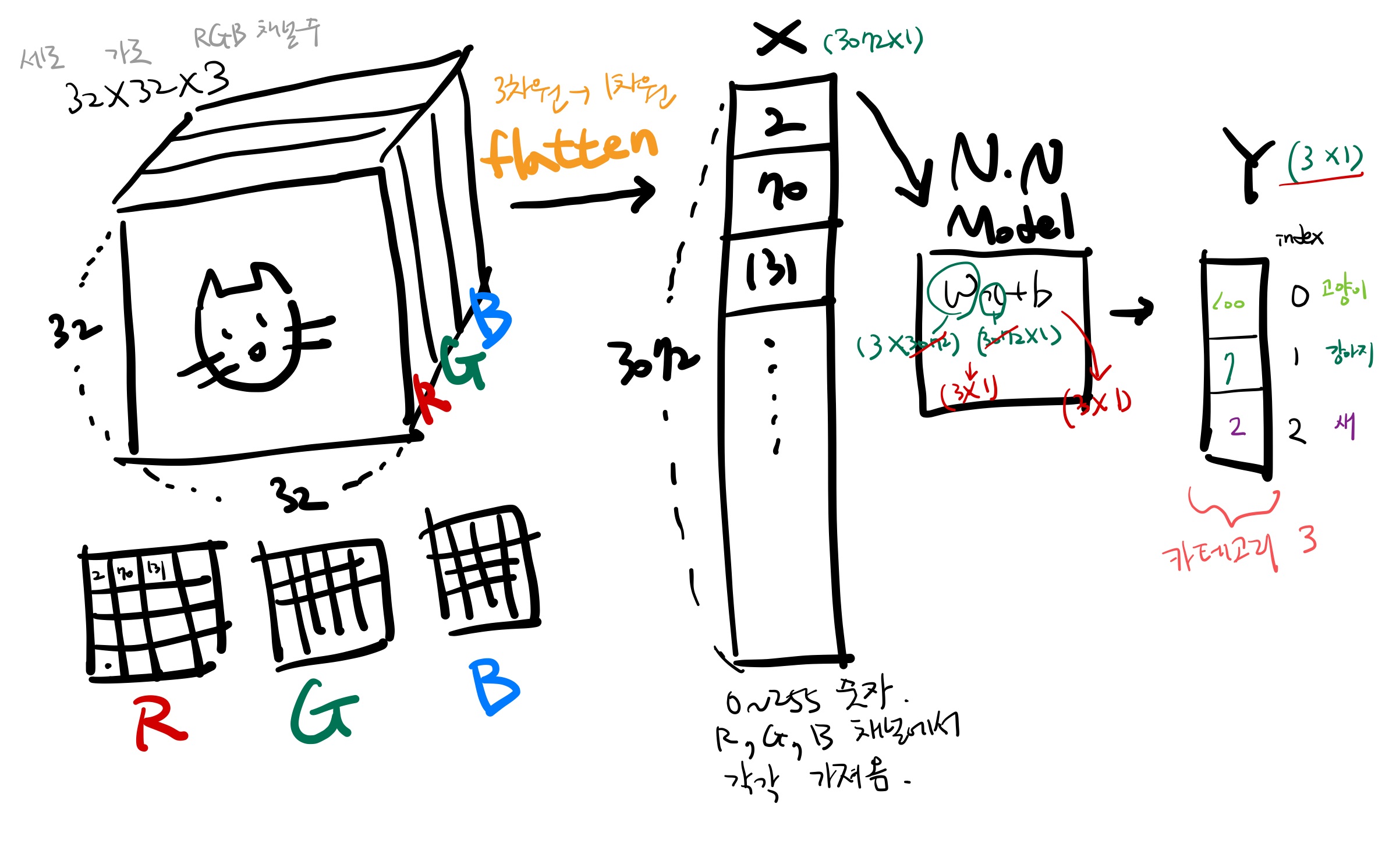

위의 그림은 W는 3행 4열, x는 4행 1열, b는 3행 1열. Wx+b를 행렬연산한 것.
(0.2×56 + (-0.5)×231 + 0.1×24 + 2.0×2) + 1.1 = -96.8 이 됨. 아래 값들도 마찬가지.
위에서는 고양이를 개로 잘못 예측함.
Wx+b가 하나의 레고블럭이고 이러한 연산이 계속해서 쌓임.
예측값 -96.8, 437.9, 61.95을 보면 내가 모르는 의미없는 값이라서 파악이 힘듦. 이것을 해결하는 것이 Softmax Function
Softmax Function
Exponential(지수로 나타낸 => 값을 극대화) - 드라마틱하게 값을 벌려준다. 지수함수는 x값이 커질수록 y값이 드라마틱하게 커짐 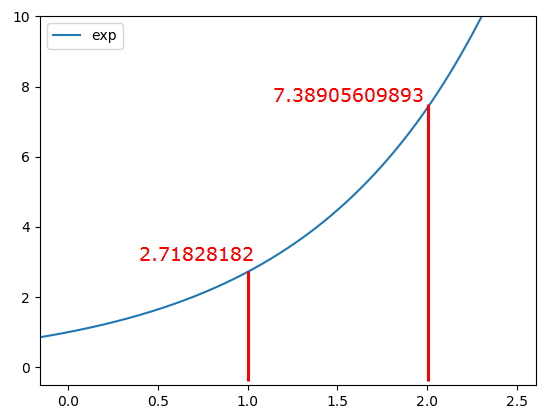 |
| Normalize(정규화) - 예측 값들을 0~1사이의 값으로 모두 정규화하며 예측 값들의 총합은 항상 1이 됨 |
Hinge Function은 Softmax Function 나오기 전에 썼던 것.
Softmax Function은 Normalize, Exponential 해서 나타냄
정규화하는데 약간의 트릭을 줌. 지수부에 e를 다 붙여주고(지수부 e는 π처럼 상수값.) 정규화함.
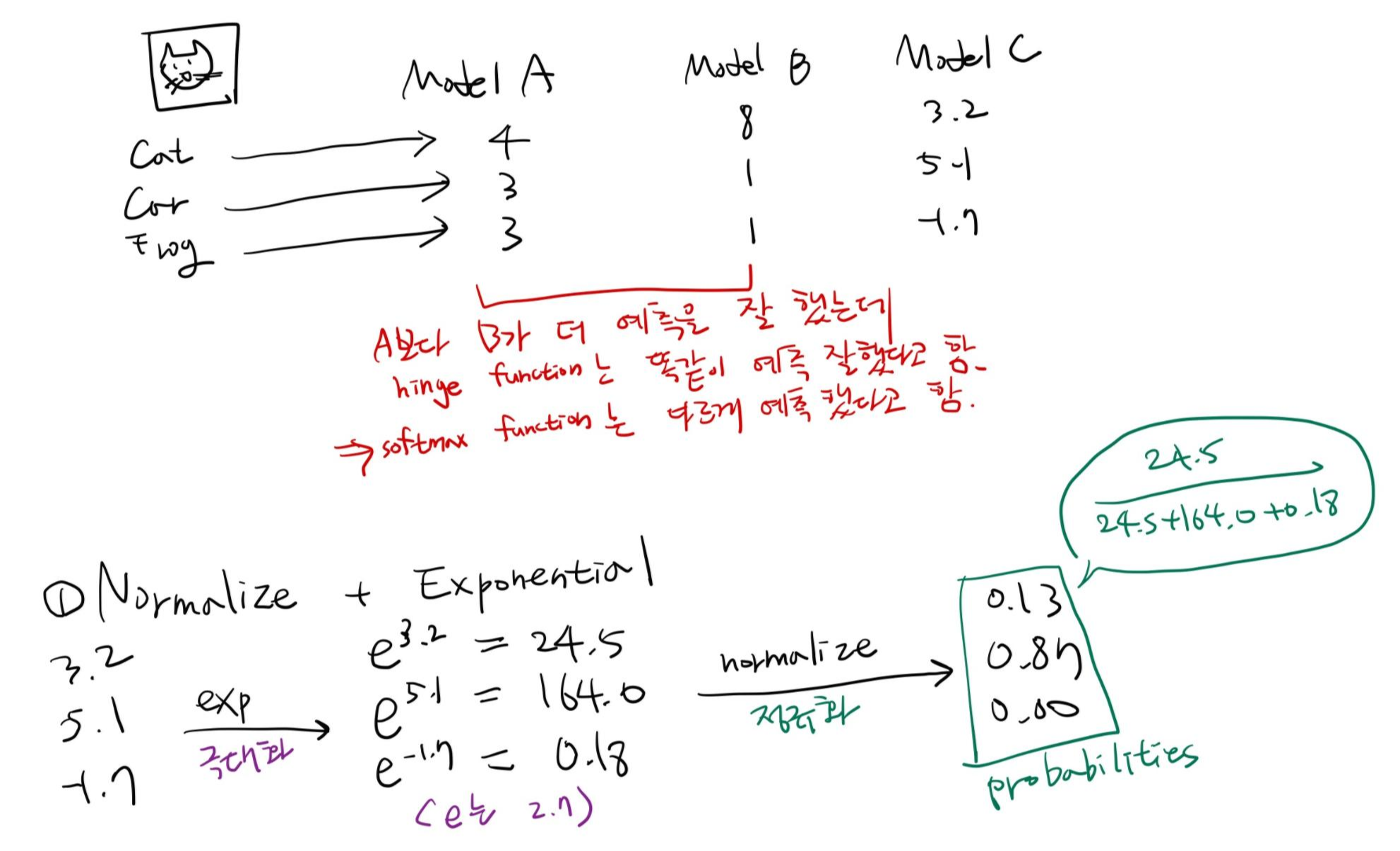
이렇게 나온 확률은 예측에 대한 평가가 아님. 예측값을 구한거지 실질적인 loss를 구한 건 아님. 예측값을 보기 좋게 0에서 1 사이의 값(다 합쳐서 1)으로 정규화한 것.
값을 예측할 때는 정확한 예측으로 안 느껴짐. 내가 얼마나 잘못한 값인지 알려면 softmax가 돌아가야 함.
Softmax Function 식 정리

Loss Function
위에서 예측한 값 0.13, 0.87, 0.00를 통해 그 때의 고도(loss)를 구한다.
x값 -> 예측한 값.
y값 -> 그 때의 고도(loss)
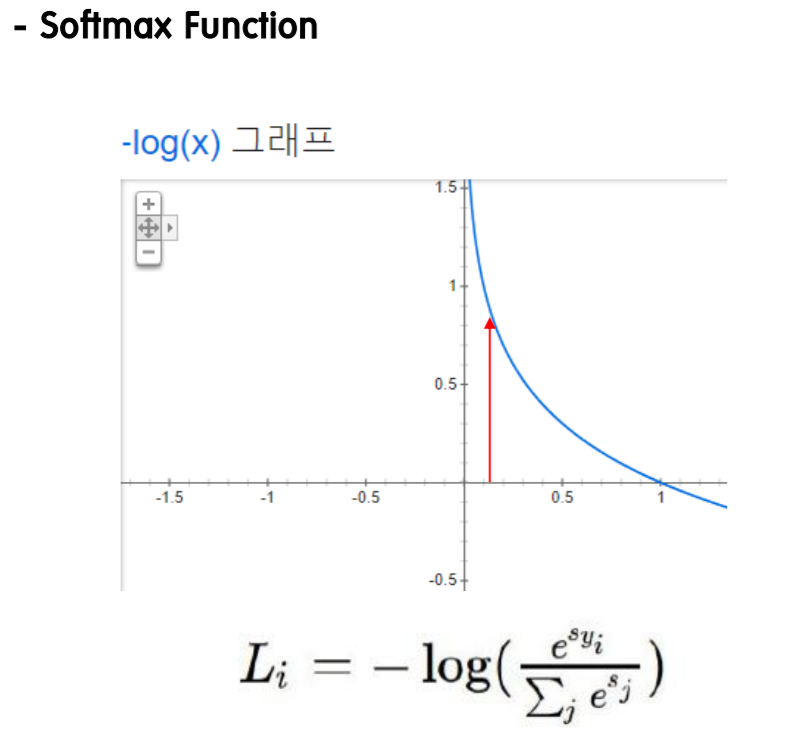

L(w)
Wx+b에 대한, 모델 전체에 대한 loss를 평가한 값
모델에 대한 loss
f(xi, w) => 예측값
y => 정답
예측값이 나오면 정답과 비교해서 loss function할 수 있다.
이미지 5만개 입력했으니 예측값 5만개 나올 거고,
총 5만개의 loss가 나올 거고, 그 loss들의 평균이 전체 Model의 loss값
모든 loss에 대한 평균값을 최종적인 loss.
=> 여기서는 트레이닝 데이터의 loss
Regularization & Full Loss Function

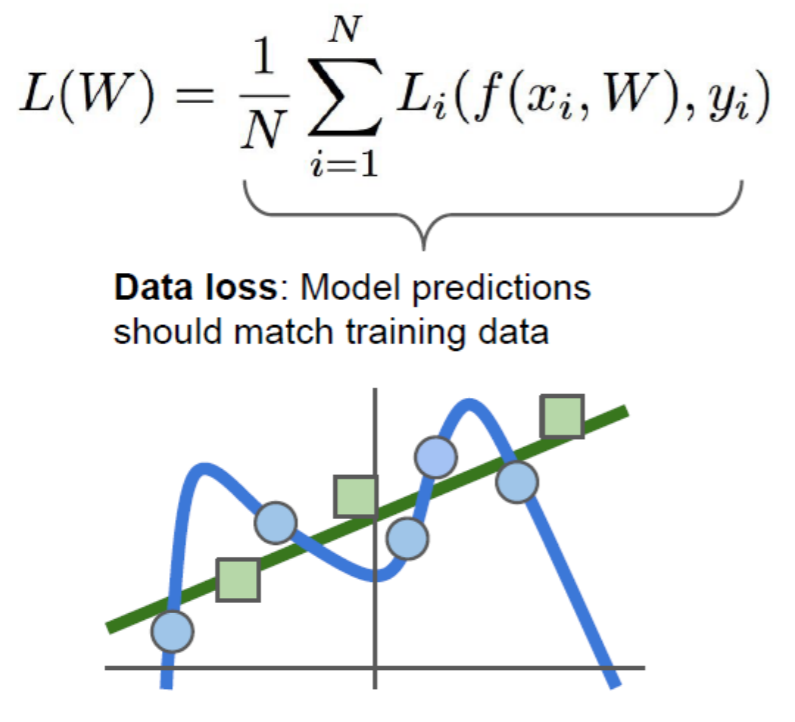
파란색이 트레이닝 데이터, 초록색이 테스트 데이터 => overfitting
Weight와 Bias에 대한, 수정치에 대한 값도 같이 구할 수 있음...
loss function을 할 때 람다(λ)라는 상수(hyperparameter임)를 앞에 붙이면 Regularization에 의해 값을 죽여주는 역할을 함. 파란색 곡선을 깎아서 초록색 선과 비슷하게 만들어줌.
람다는 overfitting을 줄여주는 역할. 널뛰는 값을 깎아서 줄여줌. 람다의 역할 => 분산의 값을 낮춰줌
Full Loss Function에는 람다까지 들어감.



W1 * x + b1 + W2 * x + b2 + W3 * x + b3 + W4 * x + b4
w 값이 작으면 굴곡이 완만해진다..

W(Weight) 값이 크면 클수록 파란색 그래프가 만들어진다. (= 데이터들의 분포가 산만하다, 안정적이지 않다, 분산이 크다 = overfitting)
W(Weight) 값이 작아질수록 연두색 그래프가 만들어진다. 훨씬 안정적인 그래프를 그림.
loss function에서 λR(w) 이 부분은 weight의 크기를 줄여주는 역할을 한다.
그렇기 때문에 Regularization을 써야 weight의 값을 안정적으로 만들어주고 overfitting을 막을 수 있다.
--> 이게 Full Loss Function

출처 : http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf




