Hayden's Archive
[AI/딥러닝] Optimization / Loss Function / Gradient Descent / Back Propagation / SGD / Neural Network 본문
[AI/딥러닝] Optimization / Loss Function / Gradient Descent / Back Propagation / SGD / Neural Network
_hayden 2020. 7. 28. 14:01Optimization(최적화) / Loss Function(손실함수) / Gradient Descent(경사하강법) / Back Propagation(오차역전파)
=> 다 연결된 개념
* 요점정리
| Optimization - 하강하는 방법 |
| Loss Function - 현재 고도를 측정하는 것 |
| Gradient Descent - Optimization 중의 하나. Back Propagation 방법을 이용해서 하산하는 Optimization - 정확한 방향을 스텝마다 계산하기 때문에 Slow, 하지만 Global Minimum까지 정확하게 찾아간다. - Learning Rate는 기본적으로 0.1을 많이 사용함. |
| Back Propagation - 가장 가파르게 내려갈 수 있는 방향을 정하는 것. 이 때 미분(실질적으로는 편미분)이 쓰임. - Weight 값이 Loss에 얼마나 영향을 주었는지를 수치화한 다음에 Loss를 가장 많이 줄이는 방향으로 Weight값을 업데이트. Loss에 영향을 많이 주었으면 책임을 많이 지고(수정값이 크고), Loss에 영향을 작게 주었으면 책임을 적게 진다(수정값이 작다) |

* Optimization -CNN에서 굉장히 중요한 개념
하산을 어떻게 해야할지, 높은 곳에서 내려갈 때 어떻게 내려가야할지 방법론에 관련된 것.
현재 고도(loss)를 알아야 Optimization을 알 수 있음.
Optimization은 어떻게 하산하는지에 대한 정의를 담고 있는데, 하산을 어떻게 하는지 알려면 현재 내 고도를 알아야 함(Loss Function)
Loss Function이 0가 되는 지점 = Global Minimum
Global Minimum처럼 보이는 가짜 평지는 Local Minimum...
로컬 미니멈에 빠지지 않고 글로벌 미니멈까지 도달하는 게 쉽지 않음.
최적의 하강 루트. 가장 빠르게 글로벌 미니멈에 도달하는 방법... 현재 고도에서 글로벌 미니멈까지 가장 가파른 경사를 찾아내는 것. Back Propagation.(이 때 내부적으로 편미분이 적용됨. x좌표가 여러개)
Back Propagation은 Loss에 따라서 기울기(Weight)를 조정함. Loss가 굉장히 높으면(예측을 잘 못함) Weight를 많이 줘야 함. Loss가 낮으면(예측을 비교적 잘함) Weight를 덜 수정함.
Back Propagation 방법을 써서 하강하는 모델이 Gradient Descent (Gradient Descent가 Optimization 중 하나임.)
Optimization
| 1) Random Search => 막 내려감. Weight 값을 무작위로 줘서 처음부터 끝까지 내려감.(운이 좋으면 빨리 끝나는데 안 좋으면 엄청 오래 걸림) -> 랜덤하게 찾으니 찾기가 힘들고 산에서 내려가기까지 시간이 너무 많이 걸림. |
| 2) Random Local Search 한발짝 내딛어서 기존의 Loss보다 낮으면 진행. 살짝 발을 뻗었더니 기존의 Loss보다 높으면 돌아옴. 이 방법 반복. Gradient Descent은 단번에 현재 Loss에서 최고의 방향을 찾아내는데 Random Local Search는 랜덤하게 한발짝 내딛기 때문에 그보다 더 좋은 방향을 놓칠 수 있음. Trial Error(시행착오)가 발생할 수 있다. => Random Search, Random Local Search는 Trial Error가 발생함. Random Local Search는 Random Search보다 Trial Error가 덜 발생하지만 Gradient Descent보다 여전히 굉장히 비효율적. |
| 3) Gradient Descent Back Propagation 방법을 써서 정확하게 편미분해서 Global Minimum까지 가장 가파른 Weight를 계산함 Gradient Descent는 가장 가파르게 Loss(고도)를 감소시키며 하강 함 =가장 가파르게 Loss(고도)를 감소시키는 Weight의 방향을 찾아냄 =가장 가파르게 Loss(고도)를 감소시키는 Weight의 방향을 Trial Error 없이 찾아내는 Optimization 방법 중의 하나이다. |
Gradient Descent 경사 하강법
p는 예측값, y는 결과값
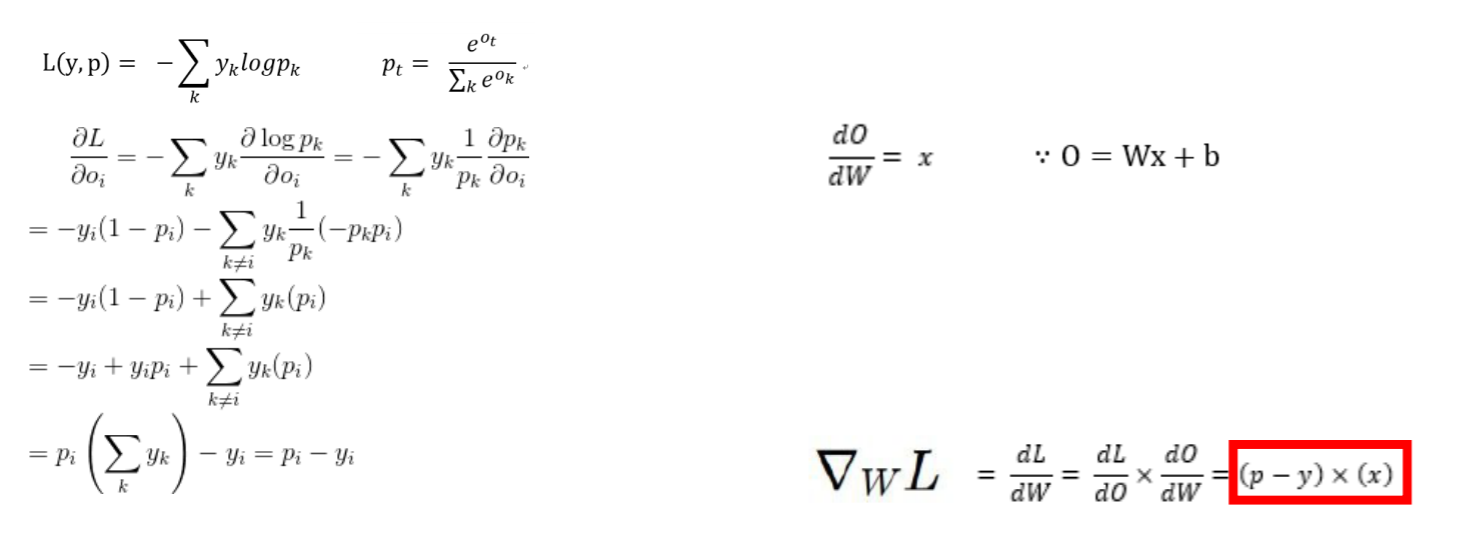



(back propagation 할 때 레이어가 수백개 수천개 나옴. 그림은 간단히 표현된 것.)
Stochastic Gradient Descent = SGD (확률적 경사하강법) & Learning Rate

위의 식에서 에타(η)는 Learning Rate를 뜻함.
기울기가 크면 빠르게 내려간다, 기울기가 작으면 천천히 내려간다.
기울기 값 자체로 속도가 결정된다.
보폭을 조절할 때, 학습 속도를 조절할 때 Learning rate를 쓰는데 이게 기울기와 같이 간다.
위는 Gradient Descent 중에서도 Stochastic Gradient Descent(SGD)임.
SGD는 천천히 가고 꼼꼼하게 찾음. 반면 Global Minimum 근처에 와서 엄청 방황하는 모델도 있음.

빨리 가고 마지막에 방황하거나, 천천히 가고 꼼꼼하게 찾거나 둘 중 하나임.
그래서 초반부에는 빨리 찾는 걸 쓰고, 학습의 마무리 단에서는 SGD처럼 꼼꼼하게 찾는 걸로 효율적이게 쓸 수 있음.
SGD 외에 여러 가지 Optimization이 있는데 대표적으로 Adam이 있음.


가장 왼쪽 그래프 => learning rate를 작게 줬을 때
가장 오른쪽 그래프 => learning rate를 크게 줬을 때
Epoch 개념

Optimizer Selection
1~10 epoch: Adam Optimizer (Fast, Rough)
10~ epoch: SGD Optimizer (Slow, Accurate)
1~10 epoch까지는 빠르게 하고, 10 epoch 이후에는 꼼꼼하게 찾는 것도 좋은 방법
Neural Network : ANN, DNN, CNN, RNN
Hidden Layer = Input과 Output 사이에 있는 레이어
Deep의 의미 Hidden Layer가 계속해서 쌓인다.
ANN - Hidden Layer가 하나
DNN - Hidden Layer가 2개 이상
CNN - DNN이지만 Convolution Layer를 씀
뉴럴 네트워크는 보통 Fully Connected Network (엣지선이 하나도 끊김 없이 다 연결됨)
Fully Connected Network

Back Propagation => CNN에서 가장 중요한 개념
뉴럴 네트워크를 통해서 예측값이 나오고, 예측값을 softmax를 통해 확률값으로 만들고, 확률값을 -log x로 해서 loss function을 만들고...
Linear Classification을 Neural Network로 나타내기






