[AI/머신러닝] 선형 회귀(Linear Regression) / 손실 함수(Loss Function) / 미분 개념 / 경사하강법(Gradient Descent)

선형 회귀(Linear Regression)

 

회귀(Regression)
- 선형 회귀( Linear Regression ) - 보통 회귀(Regression)은 선형회귀(Linear Regression)을 의미함.
- 로지스틱 회귀( Logistic Regression ) - 회귀로 풀 수 없는 문제. 분류로 풀어야 함 => 0 아니면 1로 분류. 여기서 Signoid 함수가 나옴(뉴럴 네트워크에서 인간 생체에서 나옴...)

로지스틱 회귀( Logistic Regression )

선형 회귀( Linear Regression )

 

Linear Regression에서는 Traing Data에서 보여지듯 공부시간에 대한 값 입력에 대해서 결과값인 시험성적이 연속적인 반면, Rogistic Regression에서는 입력값은 Linear Regression와 동일하더라도 결과를 이산적인 분류값으로 나타냄.

'데이터들을 표현할 수 있는 직선이 존재한다'라는 가설(Hypothesis)을 만들어낼 수 있으며 위에서는 Hypothesis가 일차함수로 나타남

 

---

손실 함수( Cost Function / Loss Function )

출처 : https://jundols.gitbooks.io/dn/content/other_chapter.html

 

위 그래프에서 빨간색 선이 예측한 값, 파란색 점이 실제값. 분홍색 선이 오차를 나타내는데, 이 격차가 좁을수록 정확도가 높다. (격차가 음의 값인지, 양의 값인지는 안 중요함. 절대값이 중요함)

예측한 값 H(x) = Wx + b 로 나타낸다. (W는 기울기, b는 y절편)

 

예측한 값과 실제값 사이의 거리를 측정하는 것이 손실 함수( Cost Function / Loss Function )이다.

(예측한 값-실제 값)을 제곱해서 다 더하고 나눠서 평균을 구함 (여기에서 m은 데이터의 개수)

(예측한 값-실제 값)을 제곱하는 이유?  1) 음수값을 없애기 위해서   2) 격차를 커지게 해서 드라마틱하게 극대화한다.(예측 못했을 때 페널티를 강하게 부여)

 

=> Cost Function은 실제적으로 w와 b에 대한 Function이다.

Linear Regression의 목적은 가장 작은 값을 가지는 W와 b를 구하는 것이다. Loss(Cost)를 0에 가깝게 낮춰야 한다.

 

---

미분(Differentiation)

 

미분 = 도함수
도함수는 미분계수를 쉽게 찾을 수 있도록 매핑해준 것.

미분 또는 도함수가 의미하는 것 -> 어떤 한점에서 그릴 수 있는 접선의 기울기 = 순간적인 변화율
미분 또는 도함수 = 접선의 기울기(순간적인 변화율)을 구하는 방법
미분의 결과 -> 미분 계수 = 도함수의 값

( 참고 : https://m.blog.naver.com/lty2242/221196988841 )

 

접선의 기울기를 구하는 이유 -> 해당 점에서 함수의 진행 방향, 변화의 정도를 알고 싶기 때문. 기울기는 얼마나 어느 방향으로 움직이냐에 대한 정보를 담고 있음.
기울기가 양수일 때 => 경사가 가파르면 -> x에 따른 y의 값이 빠르게 상승하고 있다.
기울기가 음수일 때 => 경사가 가파르면 -> x에 따른 y의 값이 빠르게 하강하고 있다.

경사가 평평할 때 => 기울기가 0 -> 이 지점이 최소점이다. 극점이라는 것을 의미함. 이 함수의 최솟값을 구하고 싶으면 미분을 해서 기울기가 0인 지점을 구하면 됨.

평균적인 변화율을 계속해서 줄여가면 그것이 바로 미분값.

상수는 변하지 않으므로 미분해도 0

 

연쇄법칙 Chain Rule
체인을 안 쓰고 거의 미분 못함. 접하는 함수의 대부분을 합성함수라고 말할 수 있음.

 

편미분 Partial Differentiation
f(x1, x2)  -> x1과 x2 둘다에 영향을 받고 있는데, x1에 대해서만 변화를 보고 싶을 때 x2를 상수화시킴. -> 이에 따라 미분은 자동적으로 x1에 대해서만 들어감
x1, x2도 둘 다에 대한 변화를 보고 싶으면 정미분이라는 개념이 들어감.

편미분한 것을 다 모으면 기울기 벡터(Gradient)

x가 하나일 때는 미분이지만 x가 여러개일 때는 편미분. 
2차원, 3차원, ... , 10000차원까지 가면 감당하기 힘들어짐.

 

 

선형회귀 Linear Regression 

=> x라는 변수에 대해서 y가 움직이고 있는데 둘 간의 관계를 보고 싶은 것. x와 y의 관계를 선형함수(y=ax+b)로 정의. a와 b가 무수히 많으니까 선형함수도 무수히 많은데 그 중에 하나. x와 y의 관계를 제일 잘 설명한 하나의 선형함수를 보고 싶고, 그래서 H(x)라는 가설회귀선을 만든다.

어떤 회귀선이 데이터를 잘 설명할 수 있을까에 대한 기준선이 필요. 실제값과 오차가 가장 작은 회귀선 하나를 고르고 싶고, 이 오차가 회귀선을 고르는 기준이 되는 것.

오차라는 게 결국 예측한 y 데이터에서 실제 y 값을 빼서 제곱한 것을 평균 낸 것. 

예측한 y 데이터에서 실제 y 값을 뺀 건 일차함수인데 제곱했으니까 이차함수가 되고 아래와 같은 형태가 나옴

미분 지점에 따라 기울기가 다 다름. 
기울기가 가파르지만 방향이 맞다면 그대로 기울기를 줄이는 방향으로 내려가본다. 

지점마다 접점을 구하는게 미분...

 

Loss Function = 오차를 제곱한 것을 1/2한 것. 2차원 함수가 미분하기 편하고, 1/2을 붙인 건 편미분 후에 나오는 2를 없애주기 위함.
최적의 기울기와 최적의 절편은 가장 작은 Loss를 가지고 있을 것이다. w에 대해서 미분.

 

---

거기서 선형으로 예측해야 함. y = Wx + b
예측하는 방법 -> 선을 그어서 예측. 기울기가 제일 중요. 내가 가장 잘 예측하는 방면으로 예측. 내가 W와 b를 써서 잘 예측... Loss가 0인 지점을 만났을 때 W와 b가 제일 정확
기울기가 0 => loss가 0인 지점.

 

경사하강법(Gradient Descent)

산에서 내려오듯이. 기울기가 크면 가파르므로 빨리 내려옴. 기울기 값에는 크기가 있고 음의 방향인지 양의 방향인지 알 수 있음. 기울기를 조정... 기울기의 값에는 크기와 방향과 속도가 모두 다 들어가 있음. 가파르게 내려온다는 건 학습을 빨리할 수 있으므로 좋은 것. 
첫번째 주어지는 기울기는 랜덤하게 주어짐. 
경사하강법에서 현재 Loss가 현재 고도. 가장 예측을 잘하는 건 고도가 0에 가까운 것. Loss가 크면 하강하면서 내려와야 함.

- 어떤 방향으로 내려갈 것인가 -> cost가 점점 줄어드는 방향으로. 이런 경사도를 따지는 게 편미분에서 따짐

(이걸 따지는 수학적 방법이 Back Propagation인데 상당히 어려움. 가장 Loss가 낮아지는, 최적의 Weight와 Bias를 찾아내는 방법론을 Back Propagation.)

현재 고도에서 Back Propagation 진행. 그럼 또 Weight와 Bias가 나옴. 아주 복잡한 공식에 의해 반복하면 정확한 지점을 찾아냄. 
선형을 여러번 긋는다 => 학습해서(=Weight와 Bias를 업데이트 해서) Loss를 보고, 학습해서 Loss를 보고, ....

Loss function이 0이 되거나 0 근처에 갔을 때 가장 정확한 W와 b를 찾아낼 수 있음.

 

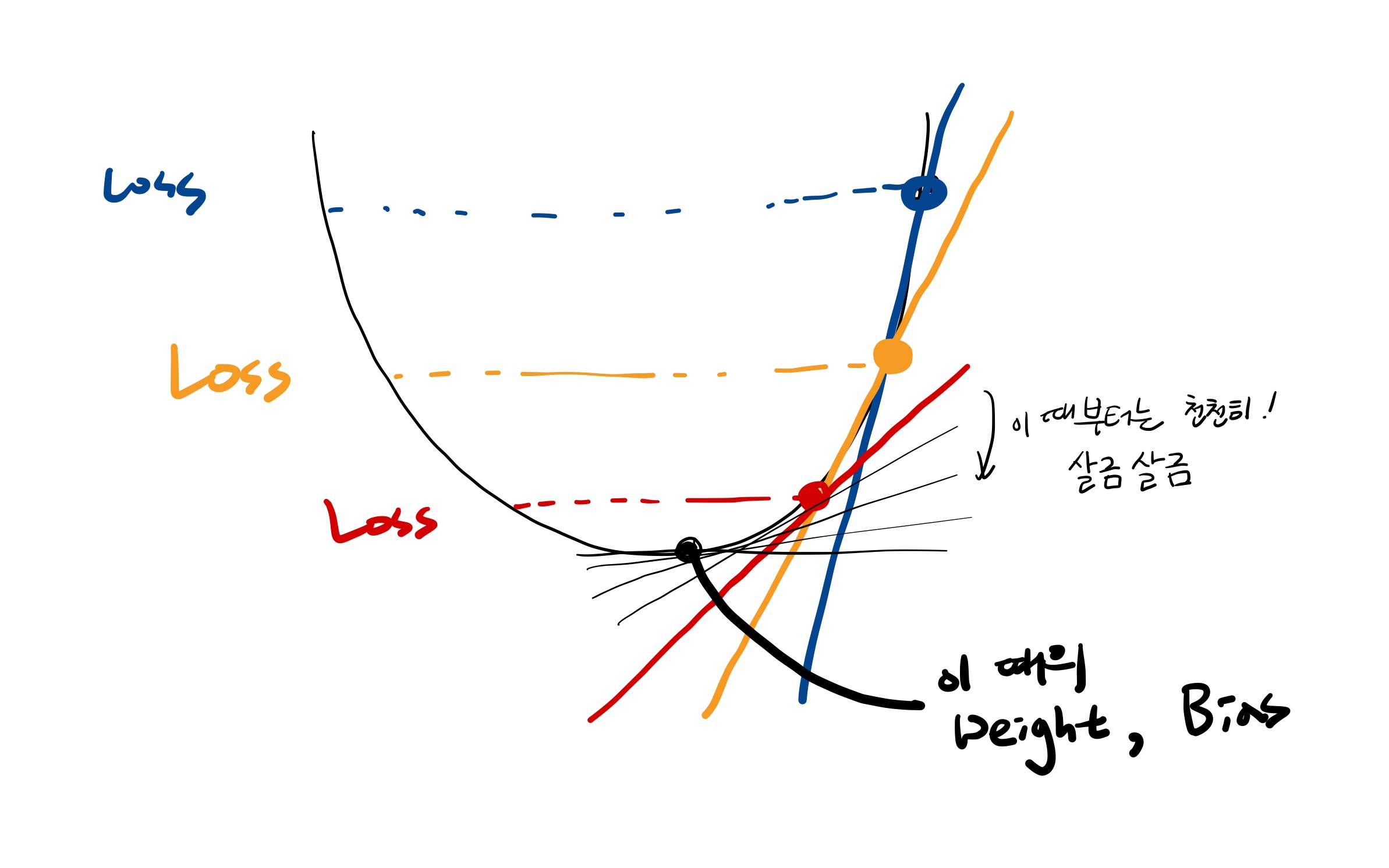
기울기가 가파르면 학습을 성큼성큼 할 수 있음. 기울기가 완만하면 Loss 지점을 정확하게 찾을 수 있음.

 

Loss Function은 크게 보면 2차함수처럼 밥그릇 모양이지만 실제로는 더 꾸불꾸불함.