[자료구조] 트리 / 이진 트리 / 이진 탐색 트리 / m원 탐색 트리 / B 트리 / B* 트리 / B+ 트리

참고 : 방통대 자료구조 강의

 

•  트리
  • 검색의 편리함
  • 논리적 계층
  • 계급적 특성

 

• 트리의 구성
  • 노드 : 트리의 항목 / 트리에 저장되는 데이터(값+포인터)의 묶음
  • 부모노드-자식노드 : 상하 계층구조가 있고 링크나 포인터를 통해 직접적으로 연결된 노드로서 상위계층의 부모노드와 하위계층의 자식노드를 뜻함 (바로 위가 아니면 조상과 자손)
  • 루트노드 : 트리의 최상위 노드(부모가 없는 노드)
  • 서브트리 : 부모 노드를 삭제하면 생기는 트리들
  • 리프노드 : 트리의 맨 끝(바닥)에 있으면서, 자신의 서브트리를 갖지 않는 노드

 

• 진입/진출 차수
  • 루트 노드 : 진입차수 = 0 (부모가 없음)
  • 루트를 제외한 모든 노드의 진입 차수 : 1
  • 리프 노드 : 진출차수 = 0 (자식이 없음)

 

• 트리의 레벨
  • 루트를 시작으로 트리를 정의하고 접근함. 루트를 기준으로 같은 레벨인지 아닌지 알 수 있음.
  • 노드의 레벨 : 루트로부터 그 노드까지 이어진 간선(경로)의 길이
  • 루트노드는 레벨 0, 그 다음 자식은 레벨 1, ... , 리프 노드는 레벨 N 이런 식

 

• 트리의 높이
  • 루트로부터 가장 멀리 있는 노드까지 이어진 간선(경로)의 길이에 1을 더한 값
  • 리프 노드가 레벨 N일 때 높이는 N+1인 것.

 

• 이진 트리(Binary Tree)
  • 따라서 모든 노드의 차수가 2 이하(0이거나 1이거나 2)인 트리 = 자식 노드가 0개 또는 1개 또는 2개
  • 수학적으로 이진트리의 구성에 관한 이론을 정리하기 쉽고, 컴퓨터 내부에서 구현하기에도 배열을 쓰든 포인터를 쓰든 유연하게 쓸 수 있음
  • 모든 노드가 2개 이하의 자식노드를 가짐 -> 일반성을 잃지 않고 '오른쪽', '왼쪽'이라는 방향 개념 부여 가능

 

• 포화 이진 트리
  • 이진 트리의 각 레벨에서 허용되는 최대 개수 노드를 가지는 트리
  • 레벨 0에서 가질 수 있는 자식노드는 최대 2개,  레벨 1에서 가질 수 있는 자식노드는 최대 4개, 레벨 2에서 가질 수 있는 자식노드는 최대 8개
  • 맨 마지막 리프노드는 제외

 

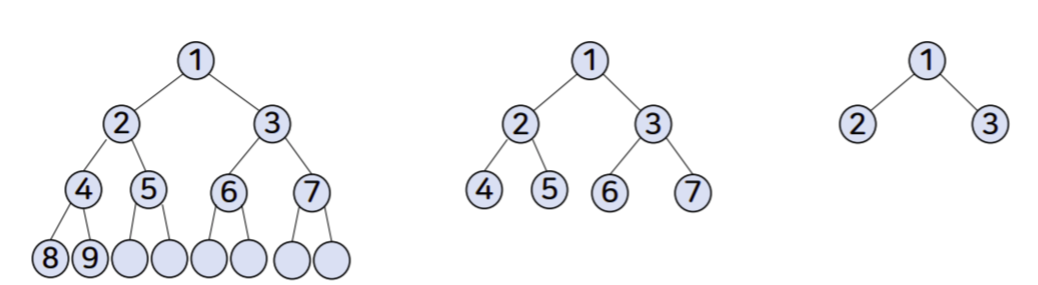
• 완전 이진 트리
  • 높이가 k인 이진 트리가 0 레벨에서부터 k-2 레벨까지 다 채우고 마지막 k-1 레벨에서 다 채우진 않더라도 왼쪽부터 순서대로 채워진 이진트리

 

• 이진 탐색 트리(BS 트리, Binary Search Tree)
  • 내가 원하는 데이터를 찾을 때 이진트리를 변형해서 이진 탐색 트리를 사용함
  • 특정 데이터를 검색하고, 노드를 삽입/삭제하는 응용 문제에 가장 효과적인 이진 트리
  • 탐색에 최적화된 이진 트리
  • 키 : 이진 트리의 노드의 데이터(노드를 특정할 수 있는 값). 노드 하나가 갖고 있는 유니크한 값을 키 값이라고 함.
  • 트리를 구성하고 구축하는 제한 사항 - 부모는 왼쪽 자식노드보다 크고, 오른쪽 자식노드보다 작다
  • 아래 그림에서 두 트리 모두 이진 트리에 해당하지만 왼쪽은 이진 탐색 트리가 맞고, 오른쪽은 이진 탐색 트리가 아니다.

 

• 이진 탐색 트리에서 일반적으로 노드의 개수가 많아지면 트리의 높이가 커지게 됨
• 트리는 탐색해서 내가 원하는 값을 찾을 때는 효율이 좋음. 하지만 재구성할 때, 트리 구조를 만들어주고 그걸 유지할 때는 오버헤드가 크다.

 

• m원 탐색 트리
  • 트리의 노드가 m개 이하의 가지를 가질 수 있는 탐색 트리
  • 이진 탐색 트리의 확장된 형태임. 높이를 줄이고자 할 때 활용.
  • 탐색 트리의 제한을 따르되 2개 이상(m개 이하) 자식을 가질 수 있음 (3원 탐색 트리, 4원 탐색 트리, ...)

 

• B 트리
  • m원 탐색 트리는 높이를 줄이는 데 집중하다 보니 균형이 안 맞음 -> 그래서 등장하게 된 게 B 트리
  • 조건
    • 루트와 잎 노드를 제외한 트리의 각 노드는 최소 (m/2보다 크거나 같은 정수)개의 서브트리를 갖는다.
    • 트리의 루트는 최소한 2개의 서브트리를 갖는다.(3원 탐색 트리라고 봤을 때, 3/2 = 1.5 니까 1.5보다 크거나 같은 정수는 2임. 따라서 트리의 루트는 최소 2개의 서브트리를 가져야 함)
    • 트리의 모든 잎노드는 같은 레벨에 있다.

 

• B* 트리
  • m원 탐색 트리에서 균형을 맞추려고 등장한 게 B 트리인데, B 트리에서 높이를 줄이는 게 또 생각나서 등장한 게 B* 트리
  • 노드의 약 2/3 이상이 채워지는 B 트리 (B 트리는 1/2 이상이었음)
  • 노드가 꽉 차면 분리하지 않고, 키와 포인터를 재배치하여 다른 형제 노드로 옮김
  • 삽입/삭제 시 발생하는 노드 분리를 줄이려고 고안됨.
  • 즉, 각각의 레벨에서의 각각의 노드들이 갖는 키 값의 개수가 많아지면 높이는 줄어든다

 

• B+ 트리
  • 탐색 트리로 구성하면 매우 빠르게 탐색할 수 있지만, 전체 데이터를 하나씩 차례로 다 찾아서 처리하기는 불편함 -> B+ 트리 등장!
  • 인덱스된 순차 파일을 구성하는 데 사용됨.
  • B 트리와 같이 각 노드의 키가 적어도 1/2이 채워져야 하는 점은 같음
  • 모든 키값이 잎노드에 있고, 그 키값에 대응하는 실제 데이터(파일 내용)에 대한 주소를 잎노드만이 가지고 있음.
    
    • 직접 탐색은 잎노드에 도달해야 종료
    • 중간노드는 잎노드까지 찾아가기 위한 징검다리 역할만 한다.

 

•  내용 정리